Брейн Ринг | Результати

Математика - 9 клас / Результати

Учасник:	Мал Тим Бог*******
Предмет:	Математика
Рівень:	9
Тривалість:	45 хвилин
Витрачено часу:	26 хвилин 30 секунд
Час початку:	2025-03-26 17:34:18
Час закінчення:	2025-03-26 18:00:48
Набрано балів:	73.67 / 100

Результат: 73.67%

Сертифікат

Запитання: #1

Розв’яжіть квадратне рівняння x2−5x+6=0. Виберіть правильний набір коренів:

$\{- 2; 3\}$

$\{2; 3\}$

$\{1; 6\}$

$\{- 3; 5\}$

Набрано балів: 3

Бали за правильну відповідь: 3

Запитання: #2

Які з наведених значень задовольняють нерівність 2x−3≤5? Виберіть усі правильні відповіді:

x=2

x=4

x=-1

x=3

x=6

— Ви відповіли правильно

— Ви відповіли неправильно

— Правильна відповідь

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #3

Заповніть пропуски у тексті, щоб отримати правильне формулювання та розв’язання задачі.

Квадратним рівнянням називається рівняння виду $a x^{2} + b x + c = 0$ , де $a, b, c$ — це коефіцієнти рівняння . Основним методом розв’язування таких рівнянь є використання дискримінанта. Формула для дискримінанта виглядає так: $D = b^{2} - 4 a c$ .

Якщо $D > 0$ , рівняння має 2 корені.
Якщо $D = 0$ , рівняння має 1 корінь.
Якщо $D < 0$ , рівняння має 0 коренів.

Набрано балів: 5

Бали за правильну відповідь: 5

Запитання: #4

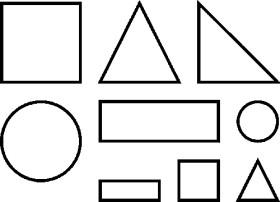
Заповніть пропуски у тексті, вибравши правильний варіант відповіді.

Якщо у трикутнику одна зі сторін є медіаною, то вона поділяє його на два рівні трикутники рівні прямокутні трикутники .
Трикутник, у якому одна зі сторін більша за суму двох інших, називається неправильної форми тупокутним .
Якщо сума двох сторін трикутника дорівнює третій стороні, то такий трикутник є невизначеним рівнобедреним .
Якщо одна зі сторін трикутника є діагоналлю його описаного квадрата, то трикутник є прямокутним рівностороннім .
Якщо кути при основі рівнобедреного трикутника дорівнюють 45° кожен, то його бічна сторона буде рівна основі більше за основу .

Набрано балів: 0

Бали за правильну відповідь: 5

Запитання: #5

Встановіть відповідність між рівняннями та їх розв'язками.

А)

2x+3=7

...

А)

...

x=2

Б)

$5 x - 1 =4$

...

Б)

...

x=1

В)

3x+4=1

...

В)

...

x=−1

Г)

4x−2=-22

...

Г)

...

x=−5

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #7

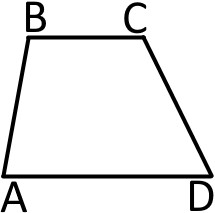
Які з наведених тверджень є вірними щодо чотирикутників? (Оберіть усі правильні варіанти)

Сума всіх кутів чотирикутника дорівнює 360°.

У паралелограмі протилежні сторони рівні.

У прямокутнику діагоналі перетинаються під прямим кутом.

У трапеції сума прилеглих кутів на одній стороні дорівнює 180°.

У ромбі всі кути рівні.

Трапеція має рівні діагоналі.

— Ви відповіли правильно

— Ви відповіли неправильно

— Правильна відповідь

Набрано балів: 5

Бали за правильну відповідь: 5

Запитання: #8

Розв’яжіть систему рівнянь:

$(\begin{matrix} 3 х - 2 у = 6 \\ 4 х + у = 9 \end{matrix})$

x=2

x=3

x=−1

x=1

Набрано балів: 0

Бали за правильну відповідь: 4

Запитання: #9

Розставте етапи розв'язання квадратного рівняння ax²+bx+c=0 у правильному порядку:


1

Підставити значення коефіцієнтів a, 𝑏, 𝑐 у формулу для дискримінанта.


2

Обчислити дискримінант за формулою $D = b^{2} - 4 a c$ .


3

Перевірити, чи існують дійсні корені (якщо дискримінант негативний, корені не існують).


4

Якщо дискримінант більший або рівний нулю, знайти корені рівняння.


5

Знайти корені за формулою $\frac{- b \pm \sqrt{D}}{2 a}$

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #10

Оцініть, чи є твердження правдивим чи неправдивим.

1.

Лінійне рівняння завжди має один корінь.

Правда

Брехня

2.

Якщо рівняння виглядає як 𝑎𝑥² + 𝑏𝑥 + 𝑐 = 0, то воно є квадратним.

Правда

Брехня

3.

Для рівняння $3 x + 5 = 0$ , корінь можна знайти, розв'язавши його через формулу дискримінанта.

Правда

Брехня

4.

Квадратне рівняння може мати один корінь, якщо дискримінант більше нуля.

Правда

Брехня

Набрано балів: 2

Бали за правильну відповідь: 4

Запитання: #11

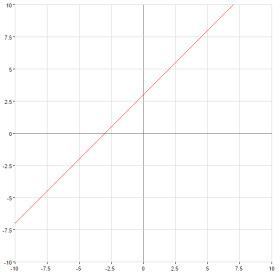
З'єднайте кожне лінійне рівняння з його графіком.

А)
y=2x+1...

А)

...
Пряма, що проходить через точку $(0, 1)$ і має нахил 2.

Б)
y=−3x+4...

Б)

...
Пряма, що проходить через точку $(0, 4)$ і має нахил -3.

В)

y= $\frac{1}{2}$ x−2
...

В)

...
Пряма, що проходить через точку $(0, - 2)$ і має нахил $\frac{1}{2}$

Г)

y=−x+3
...

Г)

...
Пряма, що проходить через точку $(0, 3)$ і має нахил -1.

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #12

Заповніть пропуски в тексті, вибравши правильний варіант відповіді.

$(\begin{matrix} a x + b y = c \\ d x + e y = f \end{matrix})$

Щоб вирішити таку систему, можна застосувати методи підстановки або додавання .
Для методу додавання треба привести рівняння до вигляду, де коефіцієнти перед $x$ або $y$ будуть однаковими. Якщо система має єдине рішення, то ці рівняння не є паралельними взаємно залежними .

Метод підстановки передбачає вираження однієї змінної через іншу, що дозволяє отримати рівняння з однією змінною. Якщо система має нескінченну кількість рішень, то рівняння будуть одночасними лінійними .

Набрано балів: 1

Бали за правильну відповідь: 3

Запитання: #13

З'єднайте кожен числовий вираз з його значенням.

А)
(5 × 3) ÷ 2 + 7 ...

А)

... 14,5

Б)
(8 × 2) − 10 ÷ 2 ...

Б)

... 11

В)
(9 + 3) × 4 − 6 ...

В)

... 42

Г)
(12 ÷ 3) + 15 − 2 ...

Г)

... 17

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #14

Визначте площу трикутника зі сторонами 6 см, 8 см і 10 см.

24 см²

30 см²

36 см²

48 см²

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #15

Заповніть пропуски в тексті запропонованими варіантами так, щоб рівняння розв'язалось правильно.

Розв'язання рівняння зовсім не складний процес. Головне - розуміти хід думок та дій. Давайте розглянемо це на прикладі.

Маємо рівняння 3x+4=2x+10. Звичайне і просте лінійне рівняння. Для того його розв'язати достатньо спочатку віднімемо 2x з обох частин рівняння. В результаті отримаємо рівняння 3x-2x +4=10. Вирішивши його отримаємо x+4=10.

Тепер віднімемо 4 з обох частин рівняння x+4-4=10-4 .

У результаті ми отримуємо відповідь, що х = 6 !

Отже розв'язати рівняння не так складно, достатьно зрозуміти основний принцип і все!

Набрано балів: 5

Бали за правильну відповідь: 5

Запитання: #16

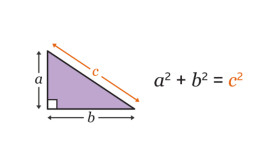
З’єднайте кожне значення сторін прямокутного трикутника з його гіпотенузою за допомогою теореми Піфагора.

А)
Сторони трикутника: 3, 4 ...

А) В)

... 5

Б)
Сторони трикутника: 5, 9 ...

Б)

... 10,3

В)
Сторони трикутника: 7, 24 ...

В) А)

... 25

Г)
Сторони трикутника: 8, 15 ...

Г)

... 17

Набрано балів: 2

Бали за правильну відповідь: 4

Запитання: #17

Оцініть правильність наведених рівностей.

1.

$\sqrt{25} = 5$

Правда

Брехня

2.

3²=9

Правда

Брехня

3.

4⁴=64

Правда

Брехня

4.

$\sqrt{16} = - 4$

Правда

Брехня

5.

2⁵=30

Правда

Брехня

Набрано балів: 5

Бали за правильну відповідь: 5

Запитання: #18

Яке з рівнянь має один корінь?

x²−5x+6=0

x²+4x+4=0

x²−3x+2=0

x²+3x+1=0

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #19

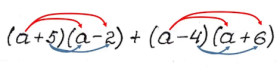
Розставте кроки спрощення виразу в правильному порядку:

(3x−2)⋅(4x+5)−(2x+3)⋅(x−1)


1

Виконати множення двочленів (3𝑥 − 2) ⋅ (4𝑥 + 5)


2

Виконати множення двочленів (2𝑥 + 3) ⋅ (𝑥 − 1)

3
4

Відняти отримані результати

4
3

Спростити отриманий вираз

Набрано балів: 2

Бали за правильну відповідь: 4

Запитання: #20

Укажіть усі правильні способи розкладання многочлена x²+5x+6 на множники.

(x+2)(x+3)

(x−2)(x+3)

x(x+5)+6

(x+1)(x+6)

𝑥(𝑥+5)

(x+3)(x+2)

— Ви відповіли правильно

— Ви відповіли неправильно

— Правильна відповідь

Набрано балів: 3.33

Бали за правильну відповідь: 4

Запитання: #21

Прочитай умову задачі і впиши правильну відповідь.

У арифметичній прогресії перший член дорівнює a1=7, різниця d=3. Знайдіть значення десятого члена прогресії (a10).

Відповідь: 34

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #22

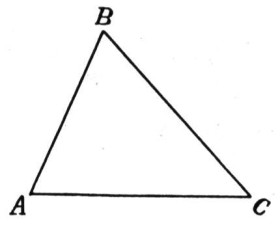
Прочитай задачу та дай відповідь на запитання.

Відомо, що в трикутнику ABC кути при вершині A та C рівні. Тобто, ∠A = ∠C. Це означає, що трикутник є рівнобедреним. Довжина основи BC становить 8 см, а одна з бокових сторін AB дорівнює 6 см.

1. Який кут В?

$60 °$

$45 °$

$90 °$

Не можна визначити

Набрано балів: 0

Бали за правильну відповідь: 4

Запитання: #23

Розмість в правильному порядку розв'язання рівняння:

1
2

6x−15+12x+4 (розкриваємо дужки)

2
1

6x+12x−15+4 (поєднуємо подібні члени)


3

18x−11 (спрощуємо вираз)

Набрано балів: 1.33

Бали за правильну відповідь: 4

Запитання: #24

Серед наведених чисел оберіть ірраціональні:

$\sqrt{2}$

4

π

3.14

$\frac{5}{2}$

$\sqrt{9}$

$\sqrt{5}$

2.75

— Ви відповіли правильно

— Ви відповіли неправильно

— Правильна відповідь

Набрано балів: 2

Бали за правильну відповідь: 4

Поділіться

Приєднуйтесь до «Брейн Ринг» у соціальній мережі Facebook!