Брейн Ринг | Результати

Математика - 10 клас / Результати

Учасник:	Кре* Іри Сер******
Предмет:	Математика
Рівень:	10
Тривалість:	45 хвилин
Витрачено часу:	44 хвилини 59 секунд
Час початку:	2025-03-30 18:23:28
Час закінчення:	2025-03-30 19:08:27
Набрано балів:	71.58 / 100

Результат: 71.58%

Сертифікат

Запитання: #1

Яке значення виразу 2x+3=11, якщо x — ціле число?

х=4

х=5

х=6

х=3

Набрано балів: 3

Бали за правильну відповідь: 3

Запитання: #2

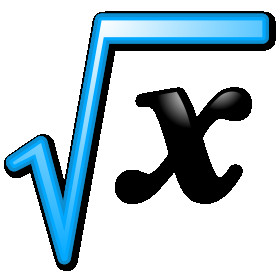
Які з наведених чисел є коренями рівняння x²−5x+6=0?

𝑥 = 1

𝑥 = 2

𝑥 = -1

𝑥 = 3

𝑥 = 0

— Ви відповіли правильно

— Ви відповіли неправильно

— Правильна відповідь

Набрано балів: 4

Бали за правильну відповідь: 5

Запитання: #3

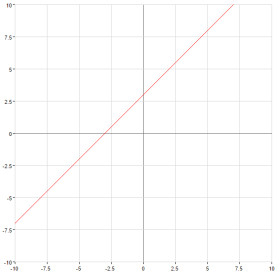
Які з наведених функцій є лінійними?

y=3x+2

𝑦 = 𝑥² + 1

y=−2x+5

y=2x³

— Ви відповіли правильно

— Ви відповіли неправильно

— Правильна відповідь

Набрано балів: 5

Бали за правильну відповідь: 5

Запитання: #4

Який перший елемент в послідовності чисел, де кожне число дорівнює попередньому помноженому на 2 і доданому до 1, якщо перше число дорівнює 1?

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #5

Розв’яжіть квадратне рівняння x2−5x+6=0. Виберіть правильний набір коренів:

$\{- 2; 3\}$

$\{2; 3\}$

$\{1; 6\}$

$\{- 3; 5\}$

Набрано балів: 3

Бали за правильну відповідь: 3

Запитання: #6

Які з наведених значень задовольняють нерівність 2x−3≤5? Виберіть усі правильні відповіді:

x=2

x=4

x=-1

x=3

x=6

— Ви відповіли правильно

— Ви відповіли неправильно

— Правильна відповідь

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #7

Заповніть пропуски у тексті, щоб отримати правильне формулювання та розв’язання задачі.

Квадратним рівнянням називається рівняння виду $a x^{2} + b x + c = 0$ , де $a, b, c$ — це коефіцієнти або коефіціенти або коефіцієнти рівняння або коефіцієнти рівняння або коефіцієнт або коефіціент сталі відомі числа . Основним методом розв’язування таких рівнянь є використання дискримінанта. Формула для дискримінанта виглядає так: $D = b^{2} - 4 a c$ .

Якщо $D > 0$ , рівняння має 2 корені.
Якщо $D = 0$ , рівняння має 1 корінь.
Якщо $D < 0$ , рівняння має 0 коренів.

Набрано балів: 3.75

Бали за правильну відповідь: 5

Запитання: #8

Заповніть пропуски у тексті, вибравши правильний варіант відповіді.

Якщо у трикутнику одна зі сторін є медіаною, то вона поділяє його на два рівні трикутники .
Трикутник, у якому одна зі сторін більша за суму двох інших, називається неправильної форми .
Якщо сума двох сторін трикутника дорівнює третій стороні, то такий трикутник є невизначеним .
Якщо одна зі сторін трикутника є діагоналлю його описаного квадрата, то трикутник є прямокутним .
Якщо кути при основі рівнобедреного трикутника дорівнюють 45° кожен, то його бічна сторона буде рівна основі менша за основу .

Набрано балів: 4

Бали за правильну відповідь: 5

Запитання: #9

Встановіть відповідність між рівняннями та їх розв'язками.

А)

2x+3=7

...

А)

...

x=2

Б)

$5 x - 1 =4$

...

Б)

...

x=1

В)

3x+4=1

...

В)

...

x=−1

Г)

4x−2=-22

...

Г)

...

x=−5

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #11

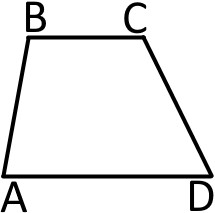
Які з наведених тверджень є вірними щодо чотирикутників? (Оберіть усі правильні варіанти)

Сума всіх кутів чотирикутника дорівнює 360°.

У паралелограмі протилежні сторони рівні.

У прямокутнику діагоналі перетинаються під прямим кутом.

У трапеції сума прилеглих кутів на одній стороні дорівнює 180°.

У ромбі всі кути рівні.

Трапеція має рівні діагоналі.

— Ви відповіли правильно

— Ви відповіли неправильно

— Правильна відповідь

Набрано балів: 4.17

Бали за правильну відповідь: 5

Запитання: #12

Розв’яжіть систему рівнянь:

$(\begin{matrix} 3 х - 2 у = 6 \\ 4 х + у = 9 \end{matrix})$

x=2

x=3

x=−1

x=1

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #13

Розставте етапи розв'язання квадратного рівняння ax²+bx+c=0 у правильному порядку:

1
2

Підставити значення коефіцієнтів a, 𝑏, 𝑐 у формулу для дискримінанта.

2
1

Обчислити дискримінант за формулою $D = b^{2} - 4 a c$ .


3

Перевірити, чи існують дійсні корені (якщо дискримінант негативний, корені не існують).


4

Якщо дискримінант більший або рівний нулю, знайти корені рівняння.


5

Знайти корені за формулою $\frac{- b \pm \sqrt{D}}{2 a}$

Набрано балів: 2.4

Бали за правильну відповідь: 4

Запитання: #14

Оцініть, чи є твердження правдивим чи неправдивим.

1.

Лінійне рівняння завжди має один корінь.

Правда

Брехня

2.

Якщо рівняння виглядає як 𝑎𝑥² + 𝑏𝑥 + 𝑐 = 0, то воно є квадратним.

Правда

Брехня

3.

Для рівняння $3 x + 5 = 0$ , корінь можна знайти, розв'язавши його через формулу дискримінанта.

Правда

Брехня

4.

Квадратне рівняння може мати один корінь, якщо дискримінант більше нуля.

Правда

Брехня

Набрано балів: 3

Бали за правильну відповідь: 4

Запитання: #15

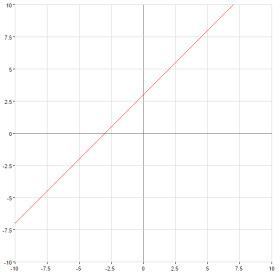
З'єднайте кожне лінійне рівняння з його графіком.

А)
y=2x+1...

А) В)

...
Пряма, що проходить через точку $(0, 1)$ і має нахил 2.

Б)
y=−3x+4...

Б) А)

...
Пряма, що проходить через точку $(0, 4)$ і має нахил -3.

В)

y= $\frac{1}{2}$ x−2
...

В) Г)

...
Пряма, що проходить через точку $(0, - 2)$ і має нахил $\frac{1}{2}$

Г)

y=−x+3
...

Г) Б)

...
Пряма, що проходить через точку $(0, 3)$ і має нахил -1.

Набрано балів: 0

Бали за правильну відповідь: 4

Запитання: #16

Заповніть пропуски в тексті, вибравши правильний варіант відповіді.

$(\begin{matrix} a x + b y = c \\ d x + e y = f \end{matrix})$

Щоб вирішити таку систему, можна застосувати методи підстановки або додавання .
Для методу додавання треба привести рівняння до вигляду, де коефіцієнти перед $x$ або $y$ будуть однаковими. Якщо система має єдине рішення, то ці рівняння не є паралельними взаємно залежними .

Метод підстановки передбачає вираження однієї змінної через іншу, що дозволяє отримати рівняння з однією змінною. Якщо система має нескінченну кількість рішень, то рівняння будуть одночасними лінійними .

Набрано балів: 1

Бали за правильну відповідь: 3

Запитання: #17

Розв'яжіть задачу:

Між двома точками на координатній площині проведена пряма, яка має рівняння 2х+х. Точка А має координти (1;5). Точка В лежить на цій прямій. Знайдіть координати точки В, якщо її абсциса дорівнює 4.

1. Яку функцію потрібно застосувати для визначення ординати точки B?

Підставити 𝑥 = 4 у рівняння прямої.

Підставити 𝑦 = 4 у рівняння прямої.

Використати формулу для відстані між точками.

Немає правильного варіанту.

Ви не відповіли на це питання.

2. Яка ордината точки B?

9

7

8

11

Ви не відповіли на це питання.

Набрано балів: 0

Бали за правильну відповідь: 4

Запитання: #18

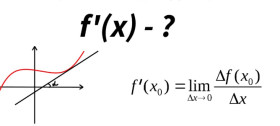
Зіставте кожну функцію з її похідною.

А)

y=x³
...

А)

...
3x²

Б)

y=sin(x)
...

Б)

...
6x

В)

y=3x²+4x
...

В)

...
6x+4

Г)

y=cos(3x)
...

Г)

...
3cos(x)

Набрано балів: 4

Бали за правильну відповідь: 4

Запитання: #19

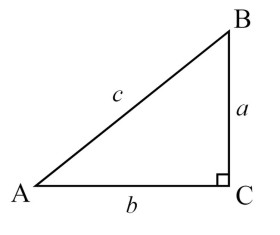
Заповніть пропуски у тексті, вибравши правильні варіанти відповідей.

Площа трикутника обчислюється за формулою S= $\frac{1}{2}$ ⋅a⋅h, де a — це довжина основи катета , а h — це висота , проведена до цієї сторони. Таким чином можна з легкістю вирішити будь-яку геометричну задачу. Наприклад, а = 12 см, а h = 8 см. Провівши розрахунок по формулі, можна дійти висновку, що площа трикутника буде 48 см².

Набрано балів: 2.67

Бали за правильну відповідь: 4

Запитання: #20

Розташуйте рівняння в порядку зростання їх розв'язку:

$2 х^{2} - 8 х + 6 = 0$

$x^{2} - 10 x + 24 = 0$

$x^{2} - 6 x + 9 = 0$

$3 x^{2} - 15 x + 18 = 0$

1
2

2x²−8x+6=0

2
1

3x²−15x+18=0


3

x²−6x+9=0


4

x²−10x+24=0

Набрано балів: 2

Бали за правильну відповідь: 4

Запитання: #21

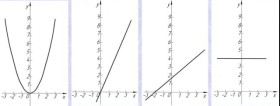
Прочитайте текст і заповніть пропуски, вибравши правильні варіанти із запропонованих.

Розглянемо функцію f(x)=ax²+bx+c. Графік цієї функції є парабола . Якщо a>0, то гілки спрямовані вгору , а якщо a<0, то гілки спрямовані вниз . Координати вершини параболи можна знайти за формулами: $- \frac{b}{2 a}$ . Ця формули важливі для аналізу властивостей квадратичних функцій .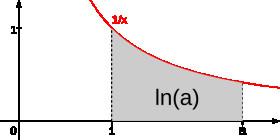

Набрано балів: 5

Бали за правильну відповідь: 5

Запитання: #22

Які з наведених тверджень є правильними щодо властивостей логарифмів?

1.

log(ab)=loga+logb

Правда

Брехня

2.

log( $\frac{a}{b}$ )=loga-logb

Правда

Брехня

3.

log(a^b)=bloga

Правда

Брехня

4.

log(a+b)=loga+logb

Правда

Брехня

5.

loga²=2loga

Правда

Брехня

6.

$log_{2} 16 = 4$

Правда

Брехня

Набрано балів: 2

Бали за правильну відповідь: 4

Запитання: #23

Розв’яжіть наступну задачу, підставляючи правильні значення в пропуски.

Відомо, що сума квадратів двох чисел дорівнює 65, а їх добуток дорівнює 24. Знайдіть ці числа.

Для розв’язання скористайтеся формулою:

$(x + y)^{2} = x^{2} + y^{2} + 2 x y$

Вираз для суми чисел: x+y= 7 113 .

Підставте значення суми та добутку чисел у квадрат рівняння: (x+y)²= 65 133 .

Розв’яжіть квадратне рівняння та знайдіть числа: x= 5 44 , y= 2 3 .

Набрано балів: 0

Бали за правильну відповідь: 4

Запитання: #24

Розставте вирази в порядку їхнього зростання результату, від найменшого до найбільшого.


1

$\frac{3}{4} + \frac{7}{8}$

2
5

$\sqrt{9} х \log_{3} (27)$

3
2

3^1/2+2^1/2


4

$\sqrt{50}$

5
3

$\log_{2} (32)$

Набрано балів: 1.6

Бали за правильну відповідь: 4

Поділіться

Приєднуйтесь до «Брейн Ринг» у соціальній мережі Facebook!